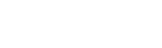وهي أهم 8 هياكل بيانات في تصميم مواقع الويب

تعد بنية البيانات طريقة خاصة لتنظيم البيانات وتخزينها على جهاز الكمبيوتر من أجل استخدام أكثر كفاءة. تمتلك هياكل البيانات مجموعة متنوعة من التطبيقات في علوم الكمبيوتر وهندسة البرمجيات. تُستخدم هياكل البيانات في جميع البرامج أو الأنظمة المستخدمة في التطوير تقريبًا. إنه مطلب أساسي في علوم الكمبيوتر ومجال تطوير البرمجيات لهيكلة البيانات. سنناقش في هذه المقالة أهم 8 هياكل بيانات في تصميم مواقع الويب.

المصفوفات

المصفوفة هي بنية ذات حجم ثابت يمكن أن تحتوي على عناصر من نفس نوع البيانات. يمكن أن تكون مجموعة من الأعداد الصحيحة ، أو عدة أرقام فاصلة عائمة ، أو سلسلة من السلاسل ، أو سلسلة من المصفوفات.

يتم تغيير حجم المصفوفة بحيث لا يمكن إزالة العناصر الموجودة في المصفوفة أو يمكن إزالتها على الفور من المصفوفة. يتم استخدامه كعنصر أساسي لإنشاء قوائم المصفوفات والمكدسات وجداول التجزئة والمتجهات وهياكل البيانات الأخرى مثل المصفوفات.

يتم استخدامه في خوارزميات الفرز المختلفة مثل إدراج الفرز ، والفرز السريع ، وفرز الفقاعة ، والفرز المدمج.

القوائم المرتبطة

القائمة المرتبطة هي بنية متسلسلة تتكون من سلسلة من العناصر ذات الصلة بترتيب خطي ، بحيث يجب الوصول إلى البيانات بشكل تسلسلي وليس عشوائيًا. توفر القوائم المرتبطة إصدارات بسيطة ومرنة من المجموعات الديناميكية.

تسمى عناصر القائمة المرتبطة بالعقد. تحتوي كل عقدة على مفتاح ومؤشر للعقدة التالية ، والتي تسمى التالي ، والعنصر الأخير من القائمة المرتبطة يسمى سلسلة

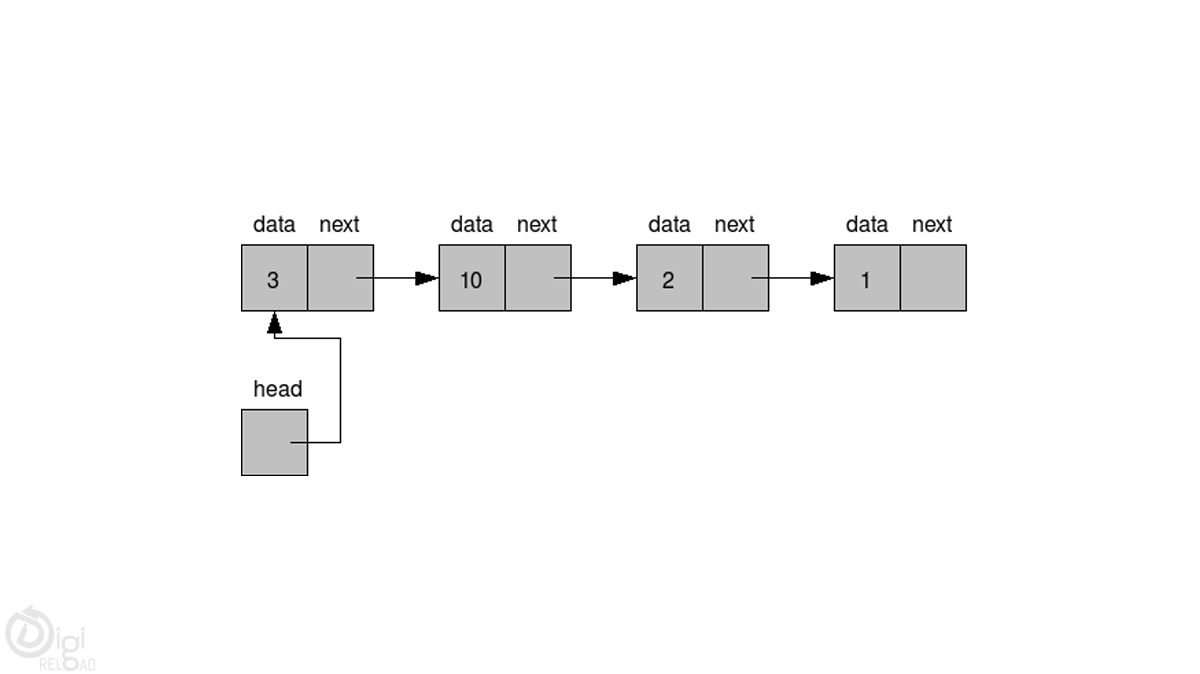
الأكوام

المكدس عبارة عن بنية LIFO مستخدمة على نطاق واسع (آخر ما يدخل أولاً يخرج أخيرًا يخرج أولاً) في العديد من لغات البرمجة. يسمى هذا التصميم "المكدس" لأنه يشبه كومة حقيقية ، كومة من اللوحات. كما يوفر الوظائف الإضافية التالية للتحقق من حالة المكدس على سبيل المثال -

• الذروة: يعرض الجزء العلوي من المكدس دون إفراغ المكدس.
• isEmpty: للتحقق مما إذا كانت الحزمة فارغة.
• IsFull: للتحقق مما إذا كانت الحزمة ممتلئة.

تُستخدم الحزم لتقييم التعبيرات الدفعية مثل خوارزميات المجال الرياضي لتحليل الصيغ وتقييمها ، كما تُستخدم أيضًا لتنفيذ استدعاءات الوظائف في البرمجة العودية.

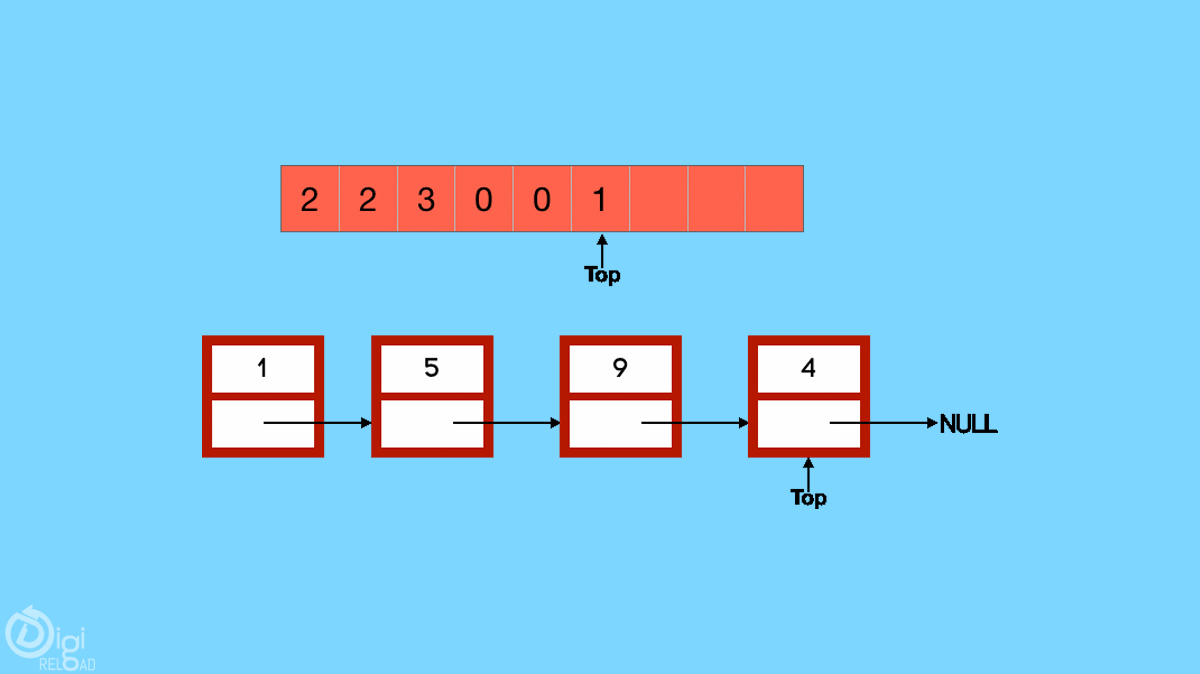
قوائم الانتظار

قائمة الانتظار هي بنية FIFO (يمكن الوصول إليها أولاً في العناصر الخارجة الأولى الموضوعة في الأعلى) ، والتي يمكن العثور عليها في العديد من لغات البرمجة. تسمى هذه البنية "قائمة الانتظار" لأنها تبدو وكأنها قائمة انتظار في العالم الحقيقي - ينتظر الأشخاص في قائمة انتظار. باستخدام قائمة الانتظار ، يمكنك إعطاء الأوامر التالية -

• قائمة الانتظار: أدخل عنصرًا في نهاية قائمة الانتظار.
• Dequeue-Remove العناصر من أعلى قائمة الانتظار.

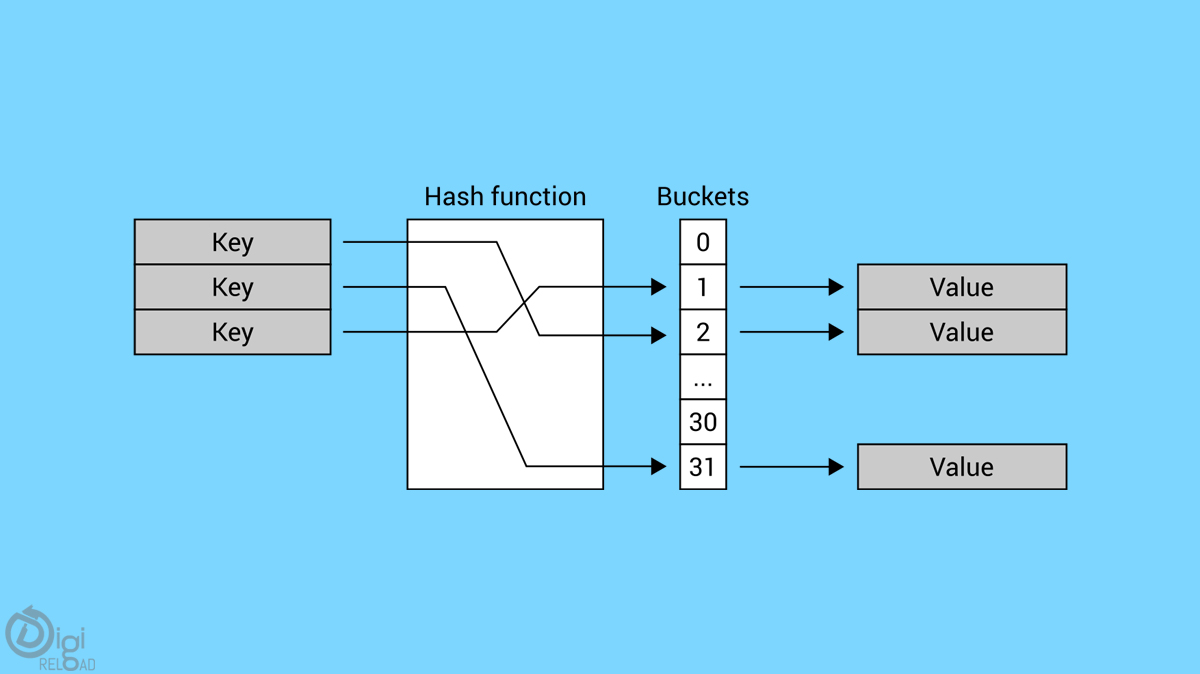
جداول تجزئة

• 

جدول التجزئة هو بنية بيانات تخزن القيم ، ولكل قيمة مفتاح مرتبط. يصبح البحث فعالاً إذا عرف المبرمج المفتاح المرتبط بالقيمة ، بالإضافة إلى البيانات التي يمكن إضافتها بأي حجم باستخدام جداول التجزئة. تستخدم جداول التجزئة تعيين واحد لواحد بين القيم والمفاتيح عند تخزينها في جدول.

ومع ذلك ، فإن هذه الطريقة تواجه مشاكل عندما يكون هناك عدد كبير من أزواج المفتاح والقيمة. تحتوي جداول التجزئة على الكثير من السجلات التي يمكن أن تشكل تحديًا لنظام الكمبيوتر العادي في تخزين تلك البيانات.

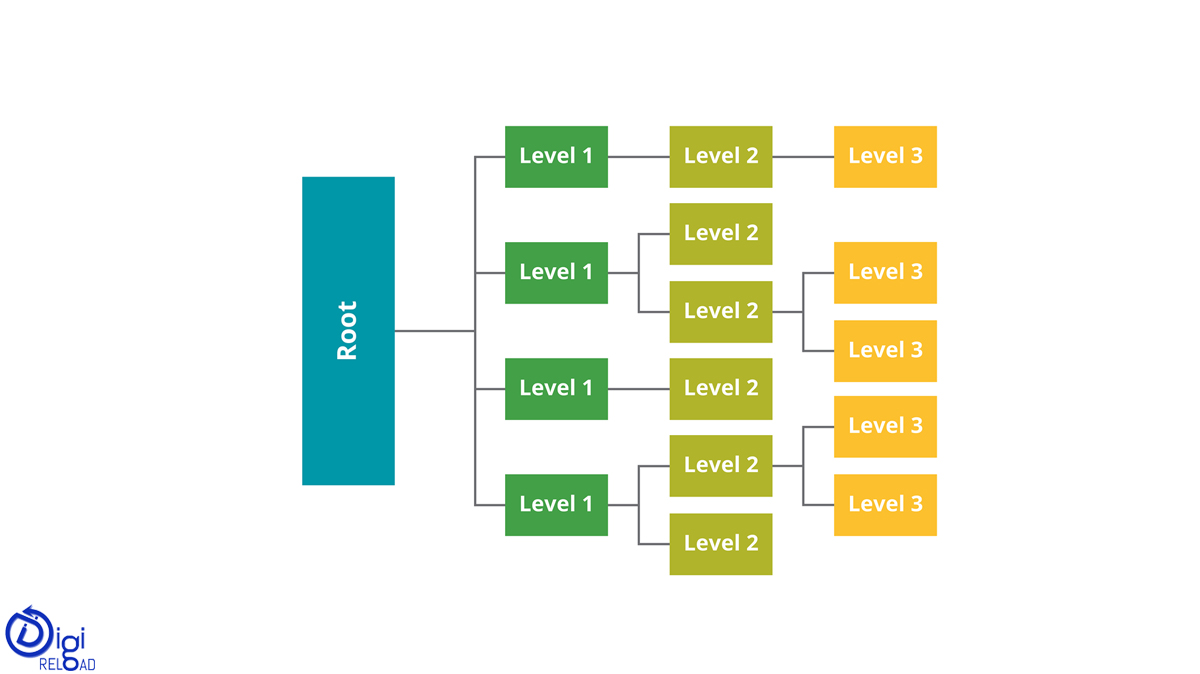
الأشجار

الشجرة عبارة عن هيكل هرمي يتم فيه تنظيم البيانات بشكل هرمي وربطها ببعضها البعض. تختلف هذه البنية عن القائمة المرتبطة ، وفي القائمة المرتبطة ، يتم ربط العناصر بترتيب خطي. في العقود القليلة الماضية ، تم تطوير أنواع مختلفة من الأشجار لتناسب تطبيقات معينة وتفي ببعض القيود.

بعض الأمثلة هي أشجار البحث الثنائية ، وأشجار B ، والصرد ، والأشجار ذات اللون الأحمر والأسود ، والأشجار الممتدة ، وأشجار AVL ، وأشجار n-ary. شجرة البحث الثنائية شجرة البحث الثنائية (BST) ، كما يوحي الاسم ، هي شجرة ثنائية حيث يمكن العثور على البيانات.

أكوام

الكومة هي حالة خاصة من الشجرة الثنائية ، حيث تتم مقارنة العقدة العلوية مع عقدها الفرعية وقيمها وترتيبها وفقًا لذلك.
مثال على الحد الأدنى من سمة الكومة هو

• الحد الأدنى من الكومة: مفتاح الأب أقل من أو يساوي مفتاح طفله. سيحتوي الجذر على الحد الأدنى لقيمة الكومة.
• الكومة القصوى: مفتاح العنصر الأصل أكبر من أو يساوي مفتاح العنصر الفرعي. وهذا ما يسمى بخاصية كومة الذاكرة المؤقتة القصوى. سيحتوي الجذر على الحد الأقصى لقيمة الكومة.

يتم استخدامه لتنفيذ قوائم الانتظار ذات الأولوية ، لأنه يمكن فرز قيم الأولوية وفقًا لسمات الكومة ، ويمكن استخدام المصفوفات لتنفيذ أكوام الذاكرة المؤقتة.

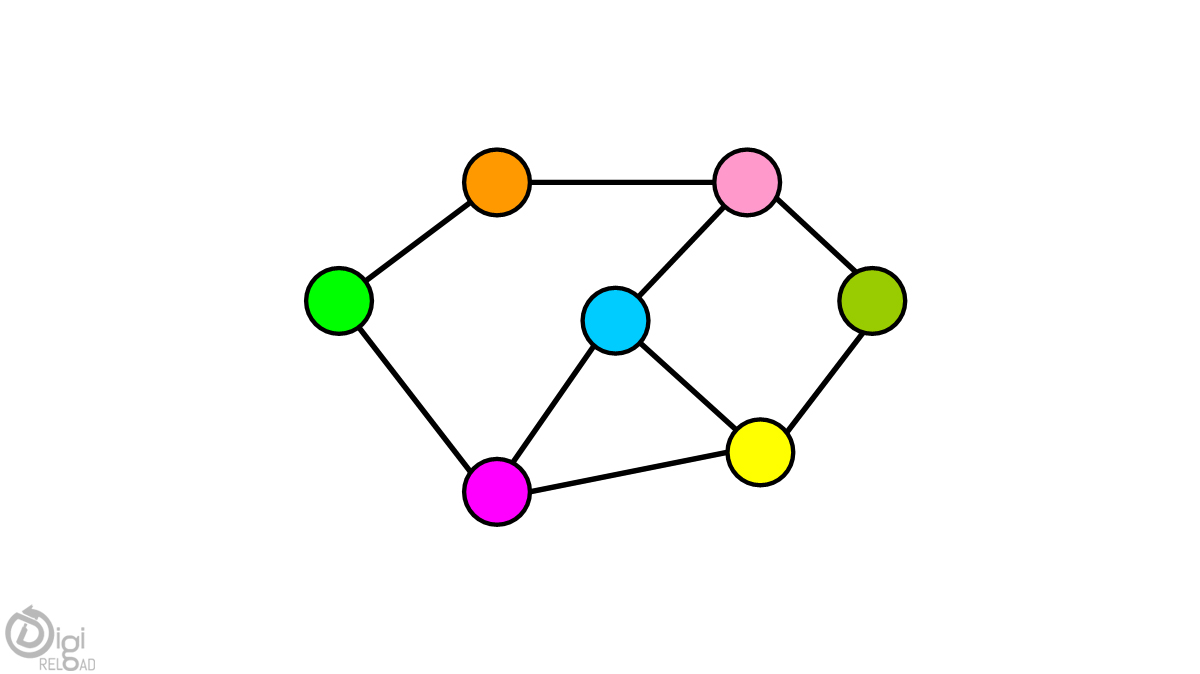
رسم بياني

يتكون الرسم البياني من مجموعة محدودة من الرؤوس أو العقد ومجموعة من الحواف التي تربط هذه الرؤوس. ترتيب الرسم البياني هو عدد الرؤوس في الرسم البياني. حجم الرسم البياني هو عدد الجوانب على المخطط. إذا تم توصيل عقدتين ببعضهما البعض بنفس الحافة ، فيُقال إن العقدتين متجاورتان.

• إذا كانت جميع حواف الرسم البياني لها اتجاه ، مما يشير إلى الرأس الأولي والرأس الأخير ، فإن الرسم البياني يسمى الرسم البياني الموجه.
• إذا لم يكن لكل حواف الرسم البياني اتجاه ، يطلق عليه رسم بياني غير موجه. يمكن أن تتحرك في كلا الاتجاهين بين رأسين.
• إذا كان الرأس غير متصل بأي عقدة أخرى في الرسم البياني ، فيُقال إنه معزول.