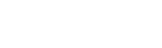ウェブサイトのデザインで8つの最も重要なデータ構造はどれですか

公開: 2022-04-28

データ構造は、より効率的に使用するためにデータを整理してコンピューターに保存するための特別な方法です。データ構造には、コンピュータサイエンスやソフトウェアエンジニアリングでさまざまな用途があります。データ構造は、開発に使用されるほとんどすべてのプログラムまたはシステムで使用されます。これは、データを構造化するためのコンピュータサイエンスおよびソフトウェア開発分野の基本的な要件です。この記事では、ウェブサイトのデザインで最も重要な8つのデータ構造について説明します。

配列

配列は、同じデータ型の要素を含むことができる固定サイズの構造体です。整数のセット、複数の浮動小数点数、一連の文字列、または一連の配列にすることができます。

配列のサイズが変更されるため、配列内の要素を削除したり、要素を配列からすぐに削除したりすることはできません。これは、行列、スタック、ハッシュテーブル、ベクトル、および行列などの他のデータ構造のリストを作成するための構成要素として使用されます。

挿入ソート、クイックソート、バブルソート、複合ソートなどのさまざまなソートアルゴリズムで使用されます。

リンクリスト

リンクリストは、一連の関連アイテムが線形の順序で構成されているシーケンシャル構造であるため、データにはランダムではなくシーケンシャルにアクセスする必要があります。リンクリストは、動的セットのシンプルで柔軟なバージョンを提供します。

リンクリストの要素はノードと呼ばれます。各ノードには、キーと次のノードへのポインタが含まれています。これはNextと呼ばれ、リンクリストの最後の要素はStringと呼ばれます。

スタック

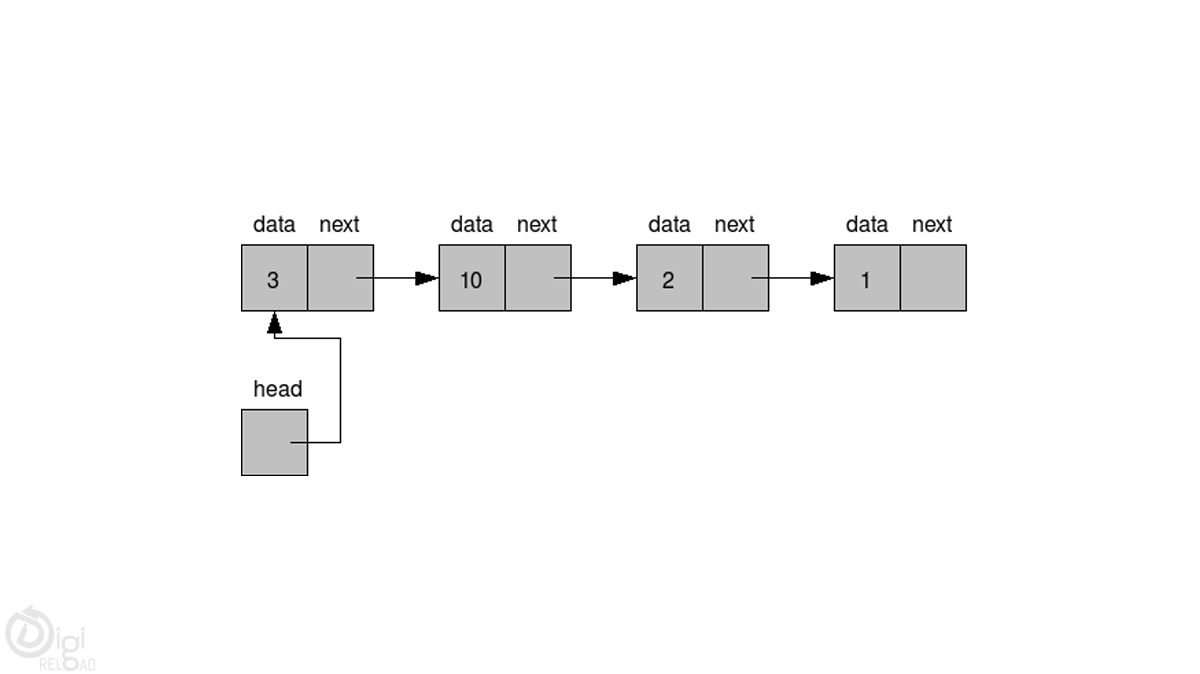
スタックは、多くのプログラミング言語で広く使用されているLIFO構造（後入れ先出し-後入れ先出し）です。このデザインは、実際のスタック、プレートのスタックのように見えるため、「スタック」と呼ばれます。また、スタックのステータスをチェックするための次の追加機能も提供します。

ピーク：スタックを空にすることなく、スタックの最上位を表示します。
isEmpty：スタックが空かどうかを確認します。
IsFull：スタックがいっぱいかどうかを確認します。

スタックは、数式を解析および評価するための数学フィールドアルゴリズムなどのバッチ式を評価するために使用され、再帰プログラミングで関数呼び出しを実装するためにも使用されます。

キュー

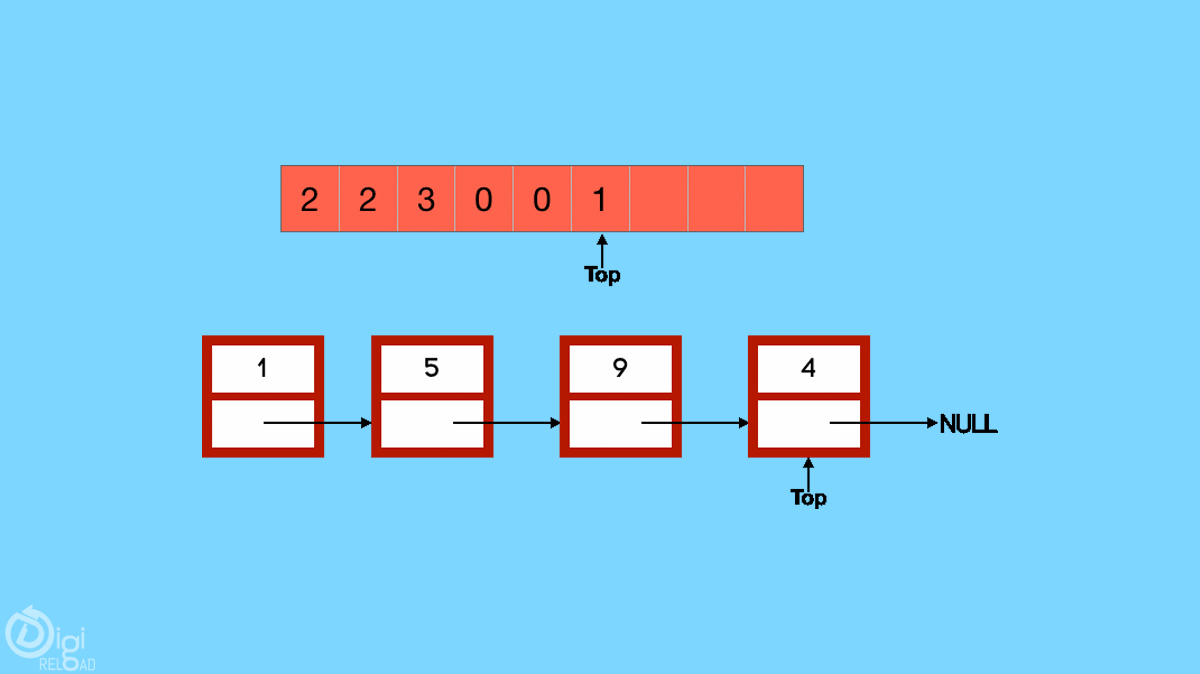
キューはFIFO（最初に最初に配置されたアイテムが最初にアクセスできる）構造であり、多くのプログラミング言語で見つけることができます。この構造は、現実の世界ではキューのように見えるため、「キュー」と呼ばれます。人々はキューで待機しています。キューを使用して、次のコマンドを与えることができます-

エンキュー：キューの最後にアイテムを挿入します。
デキュー-キューの先頭からアイテムを削除します。

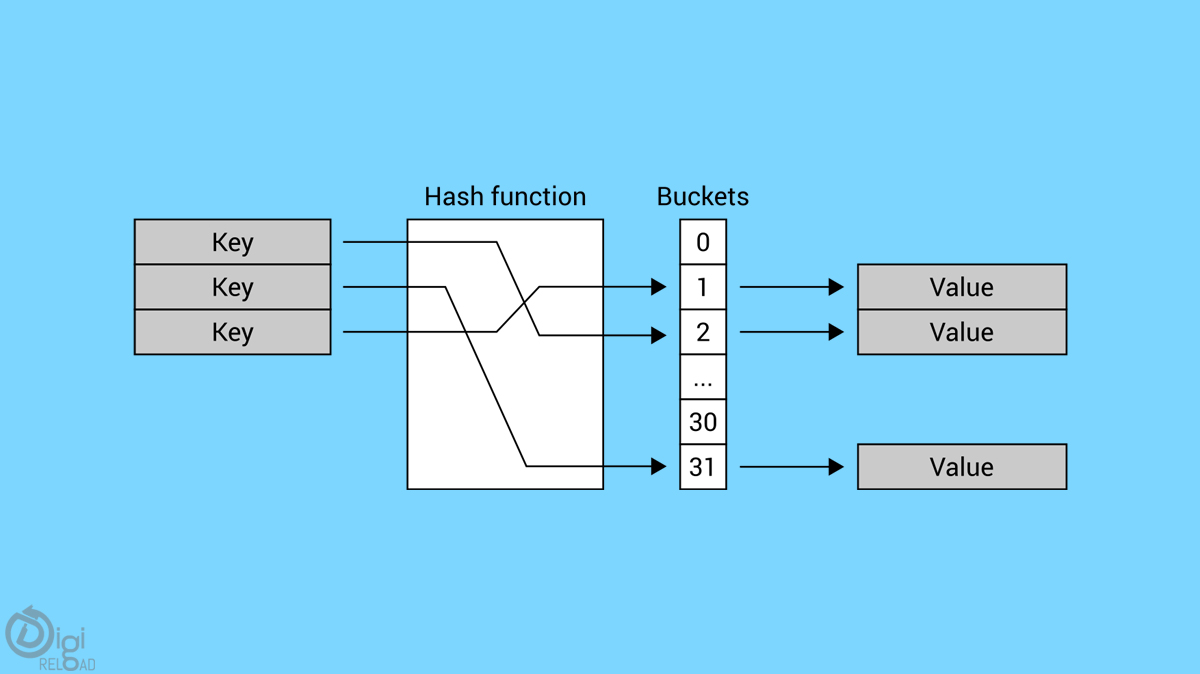
ハッシュテーブル

ハッシュテーブルは値を格納するデータ構造であり、各値には関連付けられたキーがあります。プログラマーが値に関連付けられたキーを知っている場合、検索は効率的になります。さらに、ハッシュテーブルを使用して任意のサイズでデータを追加できます。ハッシュテーブルは、テーブルに格納されるときに値とキーの間で1対1のマッピングを使用します。

ただし、この方法には、キーと値のペアが多数ある場合に問題があります。ハッシュテーブルには多くのレコードが含まれているため、通常のコンピュータシステムではそのデータを保存するのが難しい場合があります。

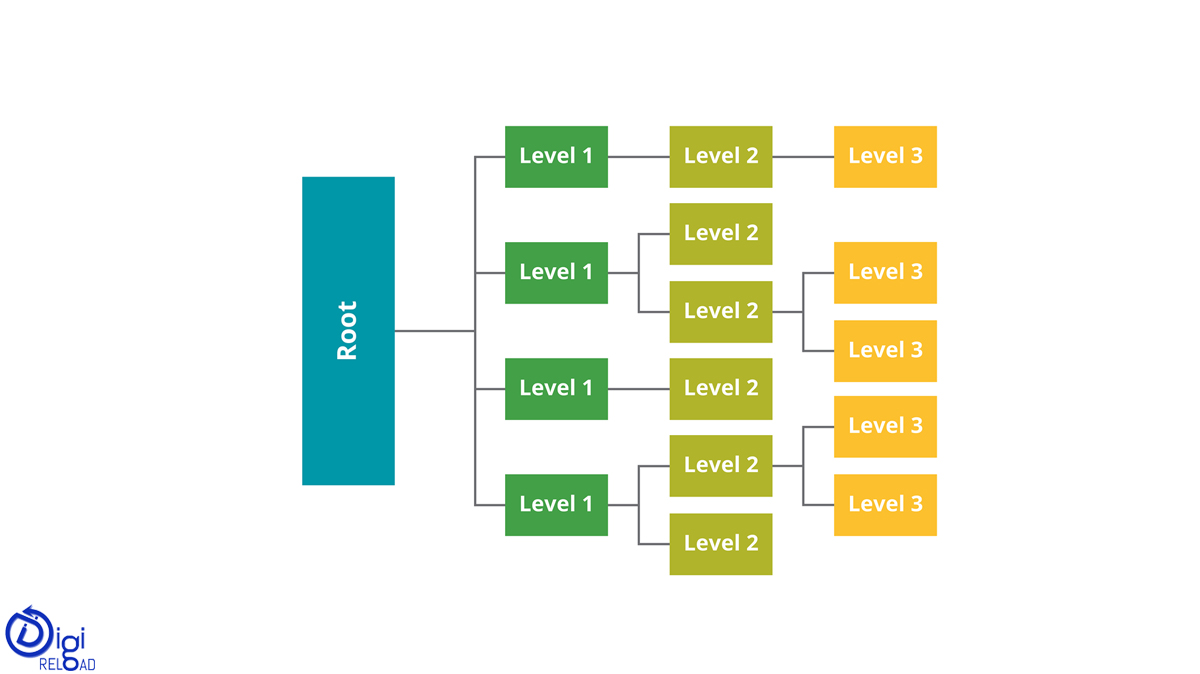
木

ツリーは、データが階層的に編成され、相互にリンクされている階層構造です。この構造はリンクリストとは異なり、リンクリストではアイテムが線形の順序でリンクされます。過去数十年の間に、特定の用途に適合し、特定の制限を満たすために、さまざまな種類の木が開発されてきました。

いくつかの例は、二分探索木、B木、treap、赤黒木、拡張木、AVL木、およびn-ary木です。二分探索木二分探索木（BST）は、その名前が示すように、データを見つけることができる二分木です。

ヒープ

ヒープはバイナリツリーの特殊なケースであり、最上位ノードがその子ノードとその値と比較され、それに応じて配置されます。
最小ヒープ属性の例は次のとおりです。

最小ヒープ：父親のキーが子供のキー以下です。 ルートには、ヒープの最小値が含まれます。
最大ヒープ：親アイテムのキーが子アイテムのキー以上です。 これは、最大ヒープ属性と呼ばれます。 ルートには、ヒープの最大値が含まれます。

優先度の値はヒープ属性に従って並べ替えることができ、配列を使用してヒープを実装できるため、優先度付きキューを実装するために使用されます。

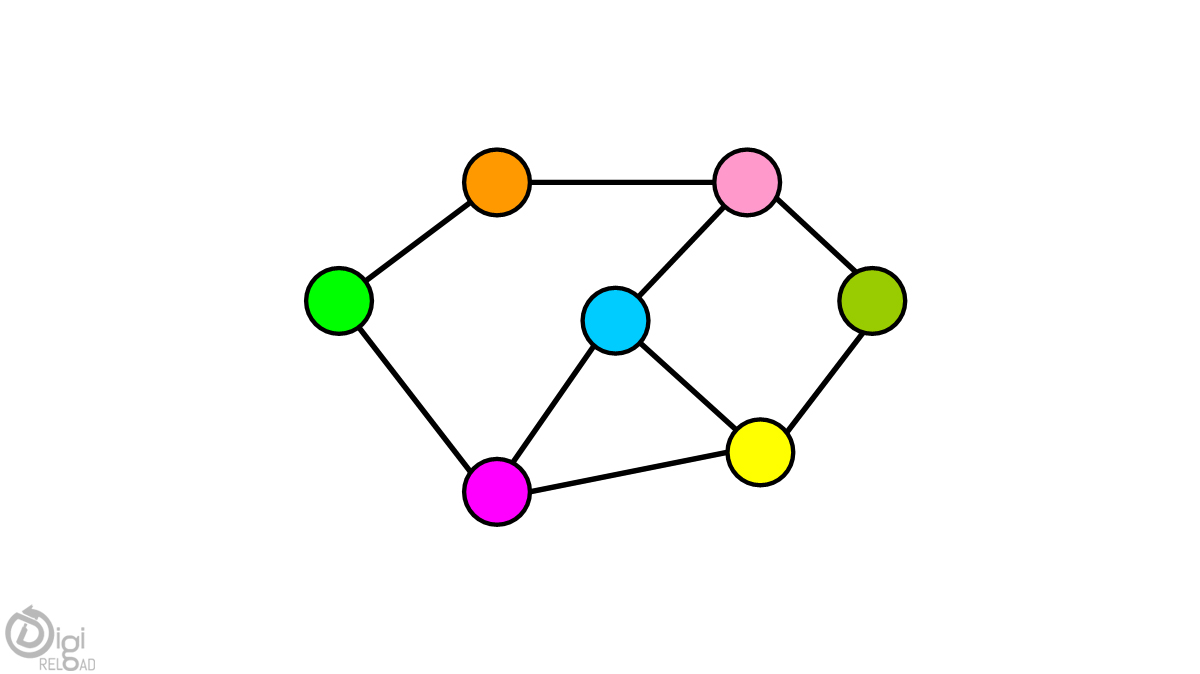
グラフ

グラフは、頂点またはノードの有限セットと、これらの頂点を接続するエッジのセットで構成されます。グラフの順序は、グラフ内の頂点の数です。チャートのサイズは、チャートの辺の数です。 2つのノードが同じエッジで相互に接続されている場合、2つのノードは隣接していると言われます。

グラフのすべてのエッジに、最初の頂点と最後の頂点を示す方向がある場合、そのグラフは有向グラフと呼ばれます。
グラフのすべてのエッジに方向がない場合、それは無向グラフと呼ばれます。 2つの頂点間を両方向に移動できます。
頂点がグラフ内の他のノードに接続されていない場合、その頂点は分離されていると言われます。