印度食品配送初創公司的漏桶
已發表: 2016-06-10[這篇文章描述了印度獨立食品配送公司的動態和單位經濟學的數學分析。 例如，為了計算每月的“消耗率”（即獨立的食品配送公司損失了多少錢），我們使用了印度特定的數字來計算配送費用和勞動力成本等。 然而，關於訂單到達率、等待時間以及它們如何影響服務水平的數學模型適用於全球]。
“外出就餐”已經結束，“點餐”開始出現。在這個新的便利經濟中，餐飲業正在學習應對這種變化，許多初創公司提供了按需向客戶提供食物的新方式。 投資緊隨其後：初創分析公司 Tracxn 顯示，2015 年印度 31 家食品科技初創公司籌集了超過 1.6 億美元，而 2014 年約為 6700 萬美元。此外，僅在 2016 年的前 15 天，一家公司就籌集了 3500 萬美元資金。 儘管有關無利可圖的傳言和最近的一些停工以及可能隨之而來的投資放緩，但資金肯定會湧入該行業。
食品配送業務受到許多現實世界因素的限制：
*交貨時間有限，因為人們通常需要在 30-45 分鐘內獲得食物，剩下 20-30 分鐘交貨（假設準備時間為 10-15 分鐘）
*不可預測的需求模式，例如，一個人可能在同一周從不同的餐廳點菜
* 點餐高峰時間高度集中，例如中午——下午 3 點吃午餐，晚上 8 點到 11 點吃晚餐，難以估計運力和管理配送車隊
*無法影響外部環境，例如交通、天氣和每天不斷變化的需求
*廚房操作
這些因素使獨立的食品配送 (FD) 初創公司難以盈利。 這些初創公司需要巨大的效率來克服現實世界的挑戰，滿足客戶的期望並實現盈利，同時還要與餐廳的內部交付支出競爭，這不是很大（並且是可自由支配的支出）。
為了迎合這種快遞需求的迅速增長，許多快遞初創公司採取了僱傭大量騎自行車的人（在印度也稱為“Field Executives”或FE），即過度投資人數來解決一個問題。問題。 假設是，雖然目前無利可圖，但食品配送業務將類似於其他配送業務（例如電子商務配送），並且最終將通過更大的訂單聚合和運營規模隨著時間的推移而盈利。 在本說明中，我們以數學方式研究這些假設。
FD業務生命中典型的一天：
考慮以下場景。
由於最近在國家報紙和電視上的報導，南德里一家受歡迎的食品配送初創公司獲得了很多訂單。 它現在每週收到超過 2000 份外賣訂單，即每小時約 40 份訂單。 一旦在系統上下訂單，它就會分配最近的可用 FE 到達餐廳，提取訂單並將其交付給客戶。 假設系統已經優化，這樣FE一到餐廳，就可以收單了。 訂單交付後，FE 將再次可用以分配給另一個訂單。 這家初創公司的首席執行官估計如下：
- 從訂單分配給FE開始，FE完成訂單的平均時間為30分鐘，即FE可以在30分鐘內開車到分配的餐廳，取餐並交付給客戶. 因此，常識表明 FE 可以以 100% 的利用率每小時交付兩個訂單。
- 為了迎合客戶，該公司聘請了 25 名 FE。 在 100% 的利用率下，他們應該能夠每小時交付 50 個訂單，遠高於 40 個訂單/小時的需求。
然而，事情並不像公司最初想像的那麼容易。 在過去的一周裡，他們被迫延遲交貨，在最後一分鐘以非常高的成本僱用額外的人，並偶爾接聽憤怒客戶的電話。
這裡發生了什麼？
外賣業務的盈利能力參數：
為了分析上面討論的情況，讓我們對整個過程進行數學建模。 以下因素對任何 FD 業務都很重要，因為它們構成了業務可能運作的數學模型的參數：
* 訂單到達率，即每小時客戶訂單數，
圖 1：客戶訂單的不同到達率
* 配送服務時間，即配送訂單的平均時間，以及
* 在任何給定時間可用的 FE 數量。
數據分析：
我們分析了 FD 業務的到貨率和服務時間相關的歷史數據，並得出以下觀察結果：
- 訂單到達率：訂單到達率不一致。 實際上，餐廳的顧客到達率可能如下所示（圖 1）：
圖 1：客戶訂單的不同到達率
為了對傳入訂單進行建模，我們假設一個馬爾科夫過程。 根據馬爾可夫過程， 潛在新客戶的數量與排隊等候的客戶數量無關。 Poisson 過程是一個眾所周知的馬爾可夫過程，通常用於模擬業務（例如食品配送業務）中的訂單到達率。 根據這個過程，每小時到達的新客戶數量由泊松分佈給出（詳見附錄1）。 定義泊松分佈所需的主要輸入參數是每小時平均到達率 (λ)，對於上面討論的示例，它等於 40 個訂單/小時。
- 送貨服務率：定義為一小時內服務的平均客戶數量。 這取決於為單個訂單提供服務所需的時間，這是一個隨機變量，由於交通狀況、餐廳/客戶等待時間等不可預測的因素。在我們撰寫本文時，我們正在從 FD 收集初始數據服務，並且服務時間似乎遵循 Gamma 分佈，平均約為 30 分鐘（即平均每小時交付 2 個訂單），標準差為 16.2 分鐘（見圖 2）。 這些服務時間包括 FE 開車到指定餐廳、取餐並將其交付給客戶所需的時間。
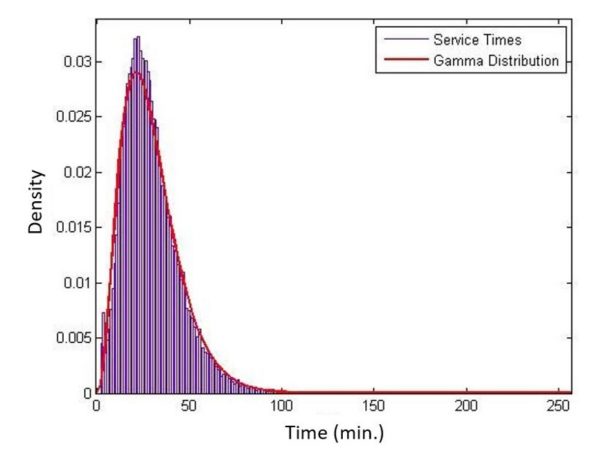
圖 2：服務時間遵循 Gamma 分佈，平均值約為 30 分鐘，標準差為 16.2 分鐘
基於上述觀察，很容易理解為什麼食品配送業務會出現排隊和等待時間增加的情況。 如果假設到達率和服務時間是統一的，即每 1.5 分鐘有一個訂單到達，並且恰好需要 30 分鐘來服務一個訂單，那麼如果我們有超過 30/1.5 ~ 20 個 FE，那麼所有訂單將是立即處理，沒有形成任何隊列。 然而，由於到達/服務率的可變性，免等待送貨服務是不可行的。
排隊系統：
現在，為了分析正在形成的隊列的行為，我們根據觀察到的數據開發了一個排隊模型，以幫助我們估計客戶在訂單送達前需要等待的平均時間。 請注意，客戶的等待時間定義為 (i) 訂單排隊時間的總和，即訂單分配給 FE 所需的時間（當所有 FE 都忙於現有訂單交付），以及 (ii) 訂單的服務時間（遵循 Gamma 分佈）。
從數學上講，為客戶分配服務器的問題屬於被稱為“排隊問題”的一類問題——從字面上看，客戶如何以不規則的時間間隔加入隊列以及如何獲得服務。 排隊論不是假設的情況：超市或公共汽車站的排隊，或者當你打電話給航空公司時一個人響應的等待時間，都遵循排隊論。
我們場景的排隊模型將具有以下結構（圖 3）：
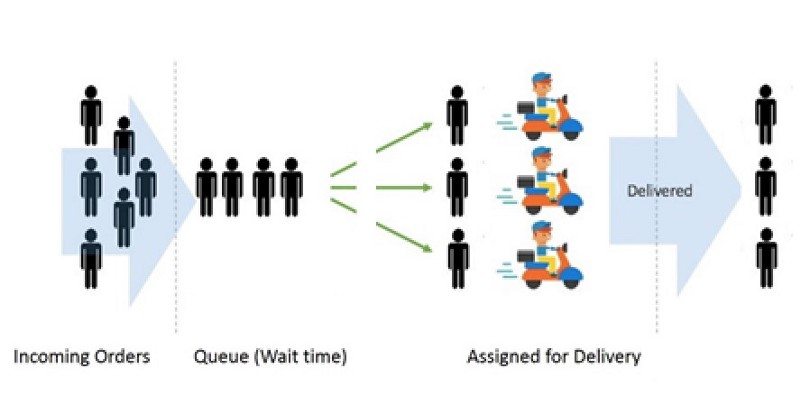
圖 3：典型的送餐流程
為你推薦：
反暴利條款對印度初創企業意味著什麼？
教育科技初創公司如何幫助印度的勞動力提高技能並為未來做好準備……
本週新時代科技股：Zomato 的麻煩仍在繼續，EaseMyTrip 發布強...
印度初創公司走捷徑尋求資金
數字營銷平台 Logicserve 獲得 80 盧比的資金，更名為 LS Dig...
報告警告對 Lendingtech Space 重新進行監管審查
- 傳入訂單：訂單隨機到達，每小時的訂單數服從均值為 λ 的泊松分佈。 排隊系統將針對不同的 λ 值進行研究。
- 隊列：隊列遵循先進先出 (FIFO) 優先級規則，並且假定容量不受限制，即外賣業務不會拒絕訂單。
- 服務：排隊系統的服務取決於FE的數量、服務費率和訂單聚合率：
- FE 的數量：我們假設它們都同樣好，並且完成訂單所需的時間相同。
- 服務率：我們知道服務時間是可變的，並且遵循平均 30 分鐘和標準差 16.2 分鐘的 Gamma 分佈。 因此，平均服務率可以計算為 µ = 2。
- 訂單聚合率：定義為所有訂單中被聚合成兩批貨物的比例，例如，當兩個訂單被聚合時，FE 能夠在一次行程中同時交付這兩個訂單。 如果訂單聚合率高，也會提高服務率。 可以很容易地得出，如果將所有訂單中的一小部分 x 聚合成對，則服務率 µ 將乘以一個因子
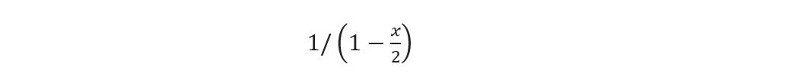
- 目前的數據表明，只有不到 5% 的訂單被聚合，這意味著更新後的服務率可以找到為 µ = 2.05。
提出的排隊模型的數學描述：
上述排隊模型可以用標準排隊命名法表示為 M/G/m 模型。 第一個字段中的“M”表示針對到達率採用馬爾可夫過程； 第二個字段中的“G”表示使用一般分佈（在我們的例子中為 Gamma）來模擬服務時間； 第三個字段中的“m”表示在排隊模型中使用了多個服務器（在我們的例子中是 FE）。
這個模型是一個有點奇怪的排隊模型，在排隊文獻中可用的分析結果很少。 根據 Lee 和 Longton (1959) 的研究論文，M/G/m 模型的平均等待時間可以通過使用一個因子來調整 M/M/m 隊列中的平均等待時間來近似。 後一種模型假設服務時間遵循指數分佈，並且是文獻中研究最充分的排隊模型之一。 下面給出的公式代表了 M/M/m 排隊系統的關鍵指標，可以很容易地推導出來：
最後，M/G/m 模型的平均等待時間可以計算為：
其中 C 是變異係數（標準差與平均值之比，我們的數據等於 0.54），W 是公式 (5) 得出的平均等待時間。
計算結果：等待時間不會線性增加
使用公式（6）計算在系統中花費的平均時間，我們可以計算不同到達率和系統平均利用率（使用公式（ 1))。 客戶的等待時間似乎隨著到達率非線性增加。 表 1 顯示了固定數量的 FE 和幾個到達率的結果。
表 1：訂單到達率、利用率和客戶等待時間呈非線性變化
這是違反直覺的：人們會認為，如果一個參數變化了大約 25%（在這種情況下，到達率從 40 上升到 50），其他相關參數，例如等待時間也會以類似的方式變化，即大概25%左右。 相反，到達率的不規則性使系統高度不穩定，並且不成比例地增加了等待時間，在這種情況下增加了 134%。
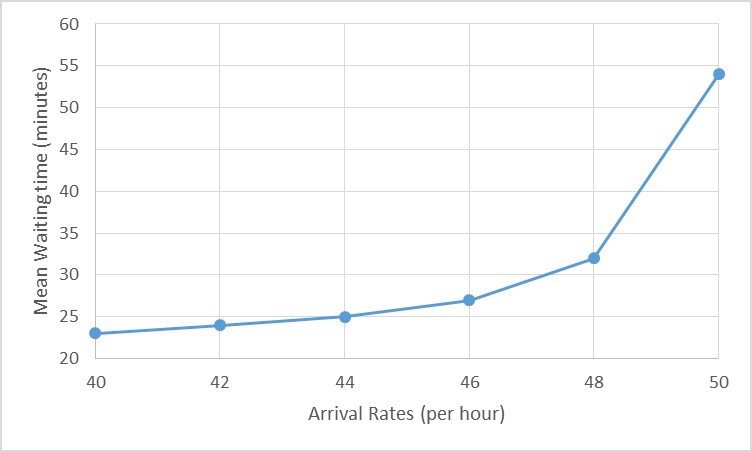
圖 4：在這種情況下，通過將客戶數量從 40 增加到 50，即僅增加 25%，平均等待時間從 23 分鐘變為 54 分鐘
對損益的影響：
表 2 顯示了我們遇到的兩種場景的 FE 工資範圍。 在大多數城市，FE 的“公司成本 (CTC)”為盧比。 每月15,000。 在班加羅爾和德里等更昂貴的大都市的某些地方，工資現在正逐漸接近盧比。 每月18,000。 請注意，FD 公司還有其他重大費用，例如燃料、自行車租賃、公司管理費用等。
表 2. 不同工資段的成本/FE
很容易理解，如果我們在地面上有更多的FE，每個訂單的平均等待時間就會減少。 我們目前承諾大約 45 分鐘的周轉時間 (TAT)。 為了始終如一地達到這一目標，平均 TAT 應在 30-35 分鐘左右，因為服務時間的標準偏差約為 16 分鐘。
讓我們看看對於不同的到達率，需要多少 FE 才能維持大約 30-35 分鐘的平均等待時間（見表 3）。 對於每個到達率，我們還展示了當我們的 FE 僅比推薦水平少一個時會發生什麼。 事實證明，平均等待時間增加到大約 55-60 分鐘。 如果我們從系統中取出另一個 FE，則交付系統變得不可行，即到達率變得超過淨服務率。 這些計算是使用公式 (6) 進行的。 表 3 還提供了在每種情況下為實現盈利而應為每個訂單收取的最低金額。
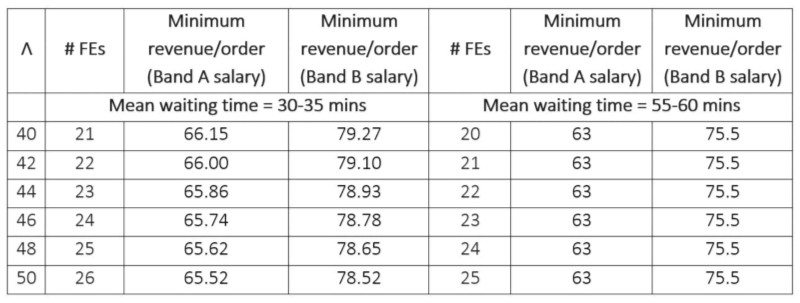
表 3：給定到達率所需的最小 FE 數量和每個訂單的相應收入要求（以盧比為單位）； Λ 代表每小時平均到達率
請注意，如果平均等待時間約為 30 分鐘（55 分鐘），則每個訂單的最低收入要求徘徊在盧比左右。 66（Rs. 63）/訂單與 Band A 員工和 Rs 左右。 79（76 盧比）/每個 B 級員工的訂單。 實際上，市場不允許我們收取超過盧比的費用。 每個訂單 50 個，因此每個訂單都會造成損失，即使我們允許 55-60 分鐘的平均等待時間，這對於送餐訂單來說可能不是可接受的周轉時間。
現在讓我們擴大計算併計算“燃燒率”，假設我們的目標是平均等待時間約為 30-35 分鐘，每個訂單的收入為盧比。 50. 表 4 顯示了兩種情況下的“燃燒率”：
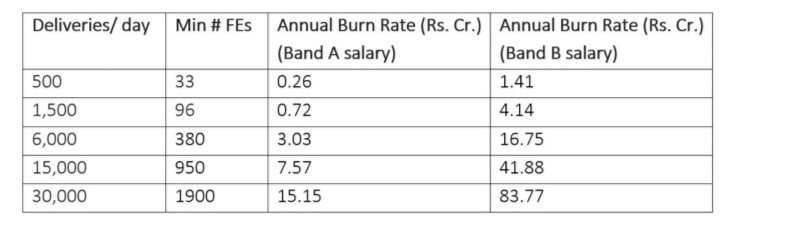
表 4：獨立 FD 公司的消耗率
關鍵假設：
請注意，為了進行本文中介紹的計算，已經做出了許多關鍵假設。 所有這些假設都有利於FD 業務，因此計算結果應被視為對實際情況的樂觀估計。 主要假設是：
- 平均到達率全天保持不變——這是極不可能的，因為實際上訂單率僅在用餐時間達到峰值。 請注意，上面討論的示例中提到的 λ = 40 的平均到達率僅適用於用餐時間。
- 系統進行了優化，FE一到餐廳就可以取餐。 實際上，這很難實現，並且經常觀察到 FE 在餐廳等待食物準備好時會浪費大量時間（平均 8 分鐘）。 出於我們計算的目的，我們假設這個等待時間是名義上的 2 分鐘，因為相信通過更好的資源調度可以避免這個等待時間。
- 如果聚合兩個或多個訂單，則 FE 交付聚合訂單所需的時間與交付單個訂單所需的時間相同。
結論：
從我們的分析可以看出，外賣業務非常不穩定，主要是因為訂單的到達率/服務率不統一。 這會導致交貨時間以及 FE 的使用率出現大幅波動，從而導致無利可圖的可能性很高。
在目前的規模下，訂單密度不是很密集，訂單很難聚合，導致大部分訂單都是“單挑單放”。 我們自己的內部數據表明，只有大約 4-5% 的訂單被匯總，這對 FD 模型的盈利能力影響不大。 但是，如果這個數字增加到 55% 左右，計算表明可以實現盈利，前提是所有其他假設仍然成立。
還有其他潛在的盈利方式，例如，通過資源的交叉利用或不同的商業模式。 一家擁有多個業務線（例如食品和包裹遞送）的公司可以交叉利用資源來建立盈利的商業模式。 例如，包裹遞送公司可以使用 FE 的包裹遞送 9-12，一些用於外賣 12-3，包裹遞送 3-6，一些用於夜間外賣。
第二種選擇是“美食俱樂部”模式，菜單有限，交貨時間有限。 這消除了等式中到達率的不確定性，從而提高了 FE 利用率。
第三種選擇是“內部送貨員”模型，其中 FE 也用於餐廳職責（例如食品服務），以降低總體交付成本並提高利用率。 實際上，大多數印度餐廳在內部都採用這種模式，因此可能值得了解其經濟學。
第四種可能的模式是用戶密度高的地方（例如班加羅爾都會區的 Koramangala），預先選擇的菜單中的食物在很短的時間內交付，類似於 UberEATS 正在試驗的東西。
獨立送餐的經濟學在於激勵科學。 如果現有 FD cos 收取的當前交付率遠低於內部承擔的成本，則企業家最終將關閉。 另一方面，如果價格上漲得足夠多，餐廳很可能會轉向內部模式。
附錄1：
了解泊松分佈：
Poisson 過程表示離散事件，例如客戶到達或電話呼叫到達交換機或呼叫中心。 如下圖 5 所示，N(t) = 時間間隔 (0,t) 內的到達次數是一個隨機變量，服從泊松分佈。
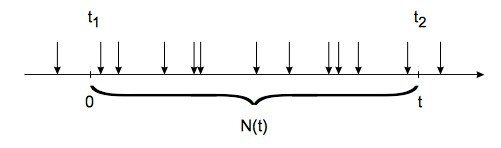
圖 5：時間間隔 (0, t) 內的到達次數
在數學上，在時間窗口 (0,t) 中獲得 N(t) = x 到達的概率可以由下式給出，
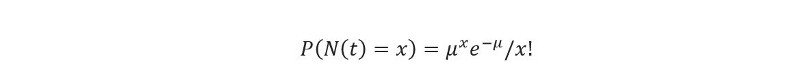
其中 µ 是時間窗口 (0,t) 中的平均到達次數。
到達間時間是獨立的並且服從指數分佈，平均到達時間 (1/ µ) 其中 µ 是每單位時間的到達率。 例如，對於每小時 40 名客戶的到達率，µ = 40。 圖 6 以圖形方式演示了這一點。
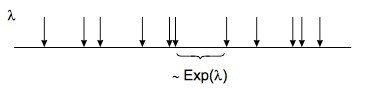
圖 6：到達間隔時間是獨立的並且服從指數分佈
結語：
在我們的首席執行官 Sahil Barua 和首席技術官 Kapil Bharati 的積極支持下，參與此職位的團隊是 Santanu Bhattacharya 博士、Kabir Rustogi 博士、Suvayu Ali（博士候選人）和 Snigdha Gupta。 全面披露，Delhivery 是印度領先的第三方物流供應商。 我們與許多 FD 公司合作，幫助他們提高效率。
作者要感謝許多審閱了這篇論文並提供了寶貴反饋的朋友，包括 Facebook 的數據科學家 Nick Berry、Multiples Equity 的 Abhi Dhall、Kotak Security 的 Ashok Tilotia 和 India Value Fund 的 Haresh Chawla。
參考：
- AM Lee 和 PA Longton，“與航空公司旅客辦理登機手續相關的排隊流程”，Oper。 水庫。 夸脫。 10：56-71（ 1959 ）
[首次發表在媒體上。]